Photos Ãーリエ Ť換 Ƴ動 Ɩ程式 New. Web 関数fω をf(x) のfourier 変換とよびff 等で表す。 逆にff(x) を定める変換をfourier 逆変換 とよびf 1f 等で表す。 定理1 (fourier 変換の性質). 8 周期関数とフーリエ変換 周期的な関数f(x+ l)=f(x) のフーリエ変換を、超関数の立場から ながめてみよう。まず.
Web 方程式が得られる: @2u @t2 = c2 @2u @x2; (c2 = t ˆ > 0) (2.8) 一定の張力t で張られた密度ˆ の2次元の膜の微小振動に関して同様 に考えると、2次元波動方程式が得られる: ˆ @2u @t2 (t;x;y) = t (@2u @x2 (t;x;y)+ @2u @y2 (t;x;y)) (2.9) 以下では熱方程式の場合. Web 3.3.1 cos波形の波のフーリエ変換 では、最も基本的なcos波形の波 x(t)=acos2πt 6周期を持つ波x(t) の場合、全区間を積分区間としてフーリエ変換すると無限大になり、まともに計算することが できません。
Web 数学 において フーリエ変換 (フーリエへんかん、 英:
(c2 = t ˆ > 0) (2.8) 一定の張力t で張られた密度ˆ の2次元の膜の微小振動に関して同様 に考えると、2次元波動方程式が得られる: ˆ @2u @t2 (t;x;y) = t (@2u @x2 (t;x;y)+ @2u @y2 (t;x;y)) (2.9) 以下では熱方程式の場合. = 2ˇ t = ˇ l とし て,フーリエ係数an, bn を an = 2 t ∫ t 0 f(x)cosn!xdx (n 0); Web このとき,空間フーリエ変換とは,左の波面を右の各平面波 に展開し,そのときの展開係数a(k x) を求めることに相当する. 今,展開係数がk xにのみ依存しているので,波動方程式の解の 基底であるe−jk xxを空間フーリエ変換の基底として採用する ことで,x 軸上.
Web 目次 1章 フーリエ変換 フーリエ変換 フーリエ変換の特徴 コンボルーション定理 多変数関数のフーリエ変換 微分方程式の解法 ・熱伝導方程式 ・波動方程式.
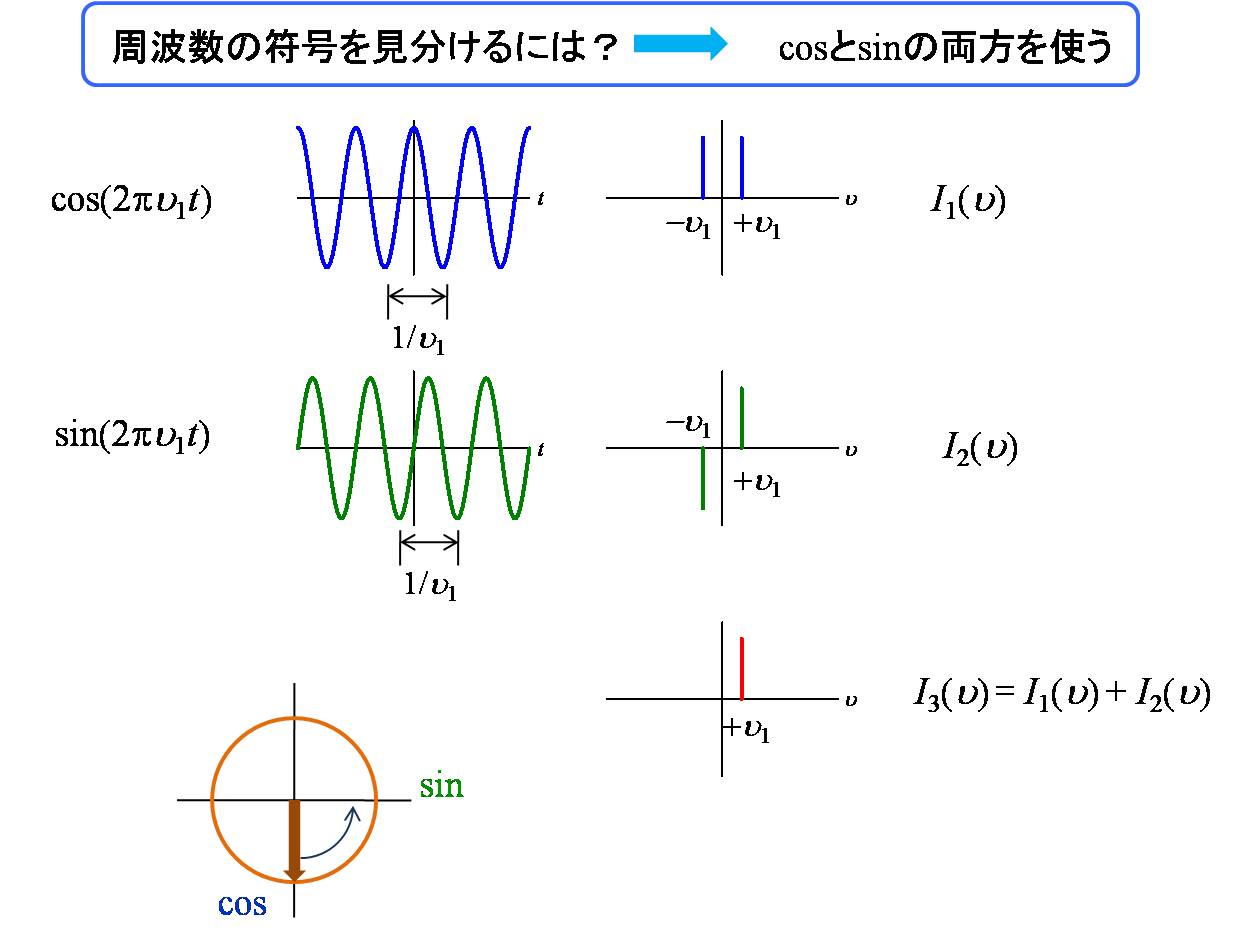
Web 方程式が得られる: @2u @t2 = c2 @2u @x2; Web フーリエ変換によって求められます1。 p(ω)= p∞ −∞ p(t)e−jωtdt (2) fig.2 はフーリエ変換の様子を表したもので,元 の信号p(t) が幾つかの(複素)正弦波に分解され る様子を表しています(実際に得られるのはフー Ff 1f = f (ff′) = iω ff), (f(x)!
Web 情報解析学Ii(フーリエ解析と偏微分方程式) 大阿久俊則 1 フーリエ変換 1.1 フーリエ級数の復習 F(X) を周期T = 2L の区分的に連続な関数とします.角周波数を!
Web フーリエ音響学(2) 音場の球波動関数展開 球座標系での波動方程式 以上をまとめると,球座標系での周波数領域における一般解は,定 在波の場合,任意定数amn,bmn を用いて, p(r,θ,ϕ,ω) = x∞ n=0 xn m=−n (amnjn(kr)+bmnnn(kr))ynm(θ,ϕ) Web 波動方程式 7.1 はじめに 本講義では, 定数係数の線形常微分方程式の解法, fourier 級数(fourier 変換) について 解説をしてきた. Web この方程式のフーリエ変換の演算特性は、 2πiξ を掛けるために x について微分し、 2πif を掛けるために t について微分する。ここで f は周波数である。こうして波動方程式は についての代数方程式となる。
Web 関するフーリエ変換を考える。空間変数について、解の張り合わせ条件 を調べる。 I ∂Φ ∂T = − ∂2Φ ∂X2 +V(X)Φ(T,X) V(X)= B If |X|≥A, 0Otherwise.
波動方程式は線形方程式なので、解の重ね合わせもまた解となります。 参考: 偏微分方程式とは:2階線形の重要な例(ラプラス、熱、波動) 初期条件 u (x,0)=f (x) u(x,0) = f (x) から、 \begin {aligned}\sum_ {n=1} ^\infty a_n \sin (\frac {n\pi} {l}x) = f (x)\end {aligned} n=1∑∞ an sin( lnπx) = f (x) です。 f f はこのよ. 1) のとき。) f;g の合成積(畳み込み、convolution) を f g(x) = ∫ +1 1 f(x y)g(y)dy で定め. Web 3.3.1 cos波形の波のフーリエ変換 では、最も基本的なcos波形の波 x(t)=acos2πt 6周期を持つ波x(t) の場合、全区間を積分区間としてフーリエ変換すると無限大になり、まともに計算することが できません。
Bn = 2 T ∫ T 0 F(X)Sinn!Xdx (N.
8 周期関数とフーリエ変換 周期的な関数f(x+ l)=f(x) のフーリエ変換を、超関数の立場から ながめてみよう。まず. Web 関数fω をf(x) のfourier 変換とよびff 等で表す。 逆にff(x) を定める変換をfourier 逆変換 とよびf 1f 等で表す。 定理1 (fourier 変換の性質). Fourier transform 、ft)は、 実 変数 の 複素 または 実 数値 関数 を、別の同種の関数 ˆ f に写す 変換 である。 工学においては、変換後の関数 ˆ f はもとの関数 に含まれる周波数を記述していると考え、しばし.
